Formulating The ReLu

Jefkine, 24 August 2016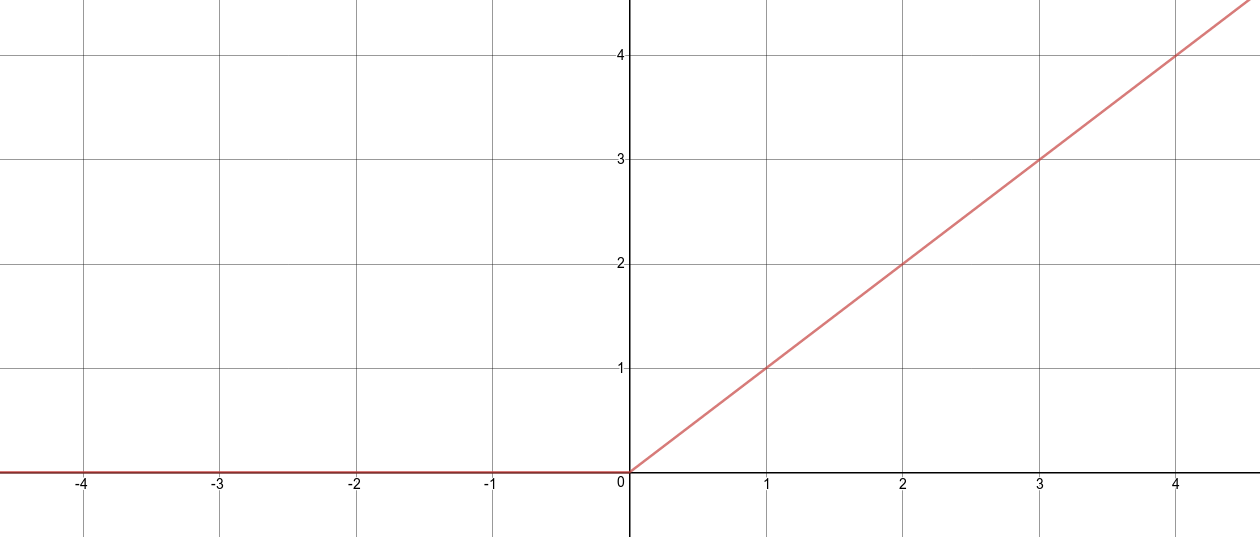

ReL Definition

The Rectified Linear Function (ReL) is a max function given by $f(x) = max(0,x)$ where $x$ is the input. A more generic form of the ReL Function as used in neural networks can be put together as follows:

$$\begin{align} f(x_i) = \begin{cases} x_i, & \text{if} \, x_i \gt 0 \\ a_ix_i, & \text{if} \, x_i \le 0 \end{cases} \tag {1} \end{align}$$

In Eqn. $(1)$ above, $x_i$ is the input of the nonlinear activation $f$ on the $i$th channel, and $a_i$ is the coefficient controlling the slope of the negative part. $i$ in $a_i$ indicates that we allow the nonlinear activation to vary on different channels.

The variations of rectified linear (ReL) take the following forms:

1. ReLu: obtained when $a_i = 0$. The resultant activation function is of the form $f(x_i) = max(0,x_i)$
2. PReLu: Parametric ReLu - obtained when $a_i$ is a learnable parameter. The resultant activation function is of the form $f(x_i) = max(0,x_i) + a_i min(0,x_i)$
3. LReLu: Leaky ReLu - obtained when $a_i = 0.01$ i.e when $a_i$ is a small and fixed value [1]. The resultant activation function is of the form $f(x_i) = max(0,x_i) + 0.01 min(0,x_i)$
4. RReLu: Randomized Leaky ReLu - the randomized version of leaky ReLu, obtained when $a_{ji}$ is a random number sampled from a uniform distribution $U(l,u)$ i.e $a_{ji} \sim U(l, u); \, l < u \, \text{and} \, l, u \in [0; 1)$. See [2].

From Sigmoid To ReLu

A sigmoid function is a special case of the logistic function which is given by $f(x) = 1/\left(1+e^{-x}\right)$ where $x$ is the input and it’s output boundaries are $(0,1)$.

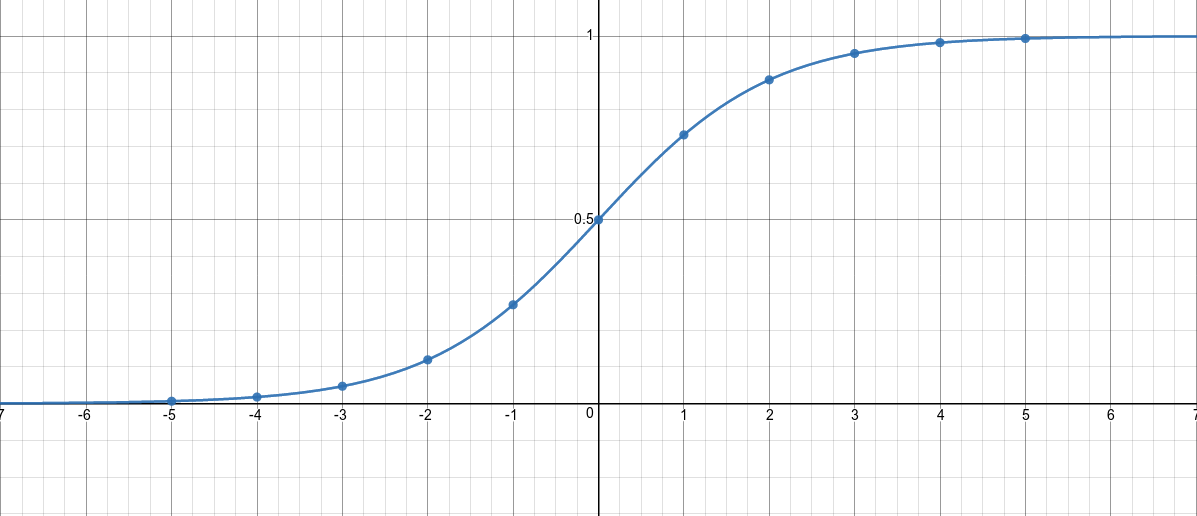
Take an in-finite number of copies of sigmoid units, all having the same incoming and outgoing weights $\mathbf{w}$ and the same adaptive bias $b$. Let each copy have a different, fixed offset to the bias.

With offsets that are of the form $0.5, 1.5, 2.5, 3.5, \dotsb$, we obtain a set of sigmoids units with different biases commonly referred to as stepped sigmoid units (SSU). This set can be illustrated by the diagram below:

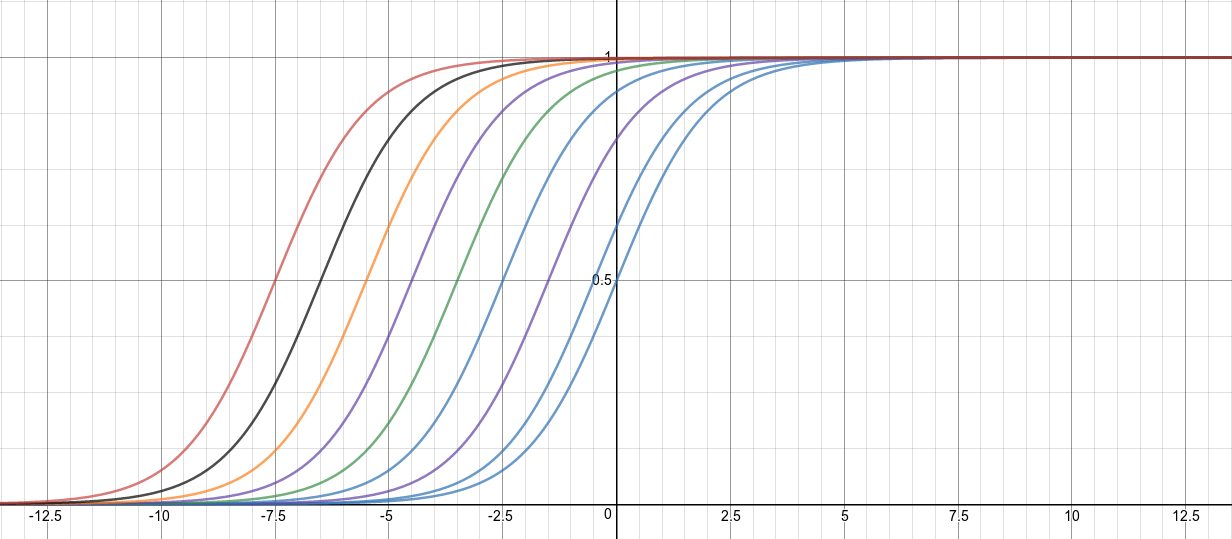
The illustration above represents a set of feature detectors with potentially higher threshold. Given all have the same incoming and outgoing weights, we would then like to know how many will turn on given some input. This translates to the same as finding the sum of the logistic of all these stepped sigmoid units (SSU).

The sum of the probabilities of the copies is extremely close to $\log{(1 + e^x)}$ i.e. $$ \begin{align} \sum_{n=1}^{\infty} \text{logistic} \, (x + 0.5 - n) \approx \log{(1 + e^x)} \tag {2} \end{align} $$

Actually if you take the limits of the sum $\sum_{n=1}^{\infty} \text{logistic} \, (x + 0.5 - n)$ and make it an intergral, it turns out to be exactly $\log{(1 + e^x)}$. See Wolfram for more info.

Now we know that $\log{(1 + e^x)}$ is behaving like a collection of logistics but more powerful than just one logistic as it does not saturate at the top and has a more dynamic range.

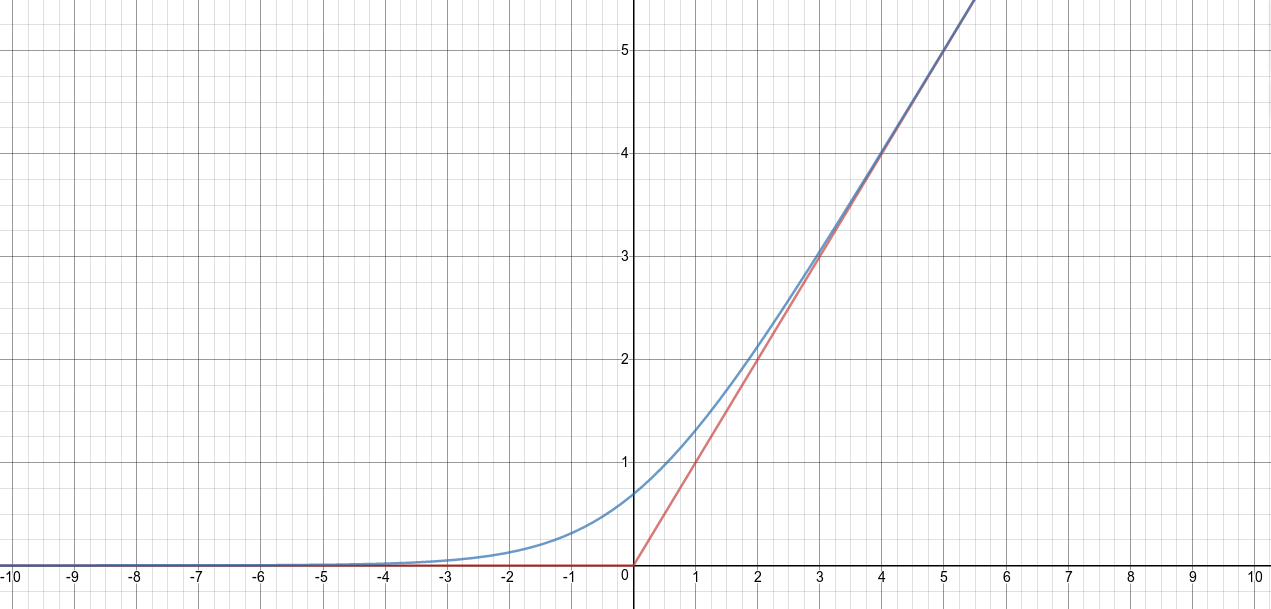
$\log{(1 + e^x)}$ is known as the softplus function and can be approximated by max function (or hard max) i.e $\text{max}(0, x)$. The max function is commonly known as Rectified Linear Function (ReL).

In the illustration below the blue curve represents the softplus while the red represents the ReLu.

Advantages of ReLu

ReLu (Rectified Linear Units) have recently become an alternative activation function to the sigmoid function in neural networks and below are some of the related advantages:

• ReLu activations used as the activation function induce sparsity in the hidden units. Inputs into the activation function of values less than or equal to $0$, results in an output value of $0$. Sparse representations are considered more valuable.
• ReLu activations do not face gradient vanishing problem as with sigmoid and tanh function.
• ReLu activations do not require any exponential computation (such as those required in sigmoid or tanh activations). This ensures faster training than sigmoids due to less numerical computation.
• ReLu activations overfit more easily than sigmoids, this sets them up nicely to be used in combination with dropout, a technique to avoid overfitting.

References

1. A. L. Maas, A. Y. Hannun, and A. Y. Ng. “Rectifier nonlinearities improve neural network acoustic models.” In ICML, 2013. [PDF]
2. Xu, Bing, et al. “Empirical Evaluation of Rectified Activations in Convolution Network.” [PDF]
3. Nair, Vinod, and Geoffrey E. Hinton. “Rectified linear units improve restricted boltzmann machines.” Proceedings of the 27th International Conference on Machine Learning (ICML-10). 2010. [PDF]